
The Golem Project
Hod Lipson and Jordan B. Pollack


|
|

|
Both the mechanics and the neural control of a machine were
simulated concurrently. The mechanics were simulated using quasi-static
motion, where each frame of the motion is assumed to be statically
stable. This kind of motion is simple to simulate and easy to
induce in reality, yet is rich enough to support various kinds
of low-momentum motion like crawling and walking (but not jumping).
The model consisted of ball-joined cylindrical bars with true
diameters. Each frame was solved by relaxation: An energy term
was defined, taking into account elasticity of the bars, potential
gravitational energy, and penetration energy of collision and
contact. The degrees of freedom of the model (vertex coordinates)
were then iteratively adjusted according to their derivatives
to minimize the energy term, and the energy was recalculated.
Static friction was also modeled. The use of relaxation permitted
handling singularities (e.g. snap-through buckling) and under-constrained
cases (like dangling bar). Noise was added to ensure the system
does not converge to unstable equilibrium points, and to cover
simulation-reality gap. Material properties modeled correspond
to the properties of the rapid prototyping material (E=0.896GPa,
r=1000Kg/m3 Syield=19MPa). The neural network was simulated in
discrete cycles. In each cycle, actuator lengths were modified
in small increments not larger than 1 cm.
Static solution of each frame is achieved by defining a global
system energy term H and then slightly modifying each of the systems
degrees of freedom so as to lower H according to its partial derivatives.
This process continues until relaxation is reached or instability
is determined. The terms included in H define the richness of
the simulation.
For example, a basic model including bar flexion and gravitational
energy would be:
![]()
where n is the number of bars, and for each bar i, m represents
the mass, h represents the average height, and the term k represents
the stiffness,
![]()
where E is the material's module of elasticity, A is the cross
section, and l is the length of the bar, and d represents the
difference between the bar's current length and its original length,
given by
![]()
and v,w represents the two current endpoints of the bar. Differentiating the total energy H with respect to each of the degrees of freedom (coordinates of the endpoints, in this case), produces direction of adjustment (second derivatives would produce a more accurate adjustment, etc.).
![]()
where Ds (the relaxation factor) represents the adjustment
magnitude for each iteration. Each degree of freedom is then updated
by its adjustment value, and H is recalculated. Small Ds produce
a stable but slower convergence, whereas large Ds can solve static
frames faster but may run into stability problems. This process
is repeated until adjustments go below a certain threshold.
Although this solution method is slower that simultaneous solutions,
(e.g. finite elements), it is capable of solving correct highly-nonlinear
cases (e.g. contact collision and snap-through buckling) and,
more importantly, under-constrained states: for example, a truss
in mid fall which is not yet fully supported (by six rigid-body
equations), as it falls into position. Indeed as machines move
and function within the simulator they often pass through such
stages. As additional real-world energy terms are added to H,
it becomes more accurate. We have included terms for friction,
collision between bars, external forces and noise.
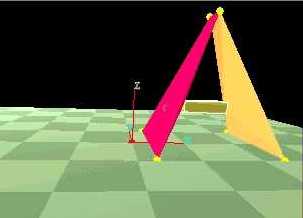
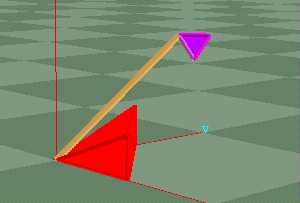
The videos below show three simulation scenes of manually-designed artifacts. On the left, a test mechanism composed of two triangular plates with a singular oscillating muscle is simulated in quasi-static motion. The motion of this test mechanism compared favorably to the physical mechanism. The two scenes on the right shows how quasi-static analysis yields pseudo-dynamic motion (even though dynamics are not accounted for in the simulation).
  |
 |
 |
|
Copyright (c) 2000 Lipson & Pollack |
lipson@cs.brandeis.edu |
Updated |