As a prototype, we have created an experimental learning environment on the Internet for the game called Tron, meeting the requirements mentioned above. First, the game is played in a Java applet window on our web site. We know that there is considerable interest in Java-based games in the Internet community, so advertising our site in some Java games lists should attract visitors. Second, our earlier experiments with Tron have shown us that, by self-play, we can produce players that are not entirely uninteresting when faced by humans. And third, each round of Tron results in a performance measure: a win, a loss or (rarely) a tie.
This means that a form of mutualism is necessary in order for an experiment such as we are proposing to be successful. Both human users and learning agents must have their own reasons and rewards for interacting. Both being adaptive species, this relationship between software agents and human users implies coadaptation of both species.
From the point of view of the learning agent species, the human environment is very noisy and adapts very fast. The evolutionary process finds its way through this noise as the better agents are being selected, slowly but surely. The motivations in this case are very simple, as rewards come from the fitness function we programmed.
People have reasons for participating that are much more complex. Fun, curiosity, competition against an unfamiliar intelligence, and competition against each other to appear in the `ranking' page are among them. The evolutionary properties of the animat population create a changing artificial environment that makes people come back searching for a renewed challenge.

2. Tron
Tron, a 1982 movie from Walt Disney Studios, shows a game in a virtual world where two futuristic motorcycles run at constant speeds, making only right angle turns and leaving solid wall trails behind them. As the game advances, the arena fills with walls and eventually one opponent dies by crashing into a wall. This popular game has been implemented on all kinds of computers with varying rules and configurations.
We have built a version of Tron using a Java applet and released it on the Internet. In our interpretation, the motorcycles are abstracted and represented only by their trails. Two players (one human, one animat) start in the middle region of the screen, moving in the same direction (fig. 2). The edges of the arena are not considered "walls"; players move past them and reappear on the opposite side, thus creating a "wraparound", or toroidal, game arena. The size of our arena is 256×256 pixels.
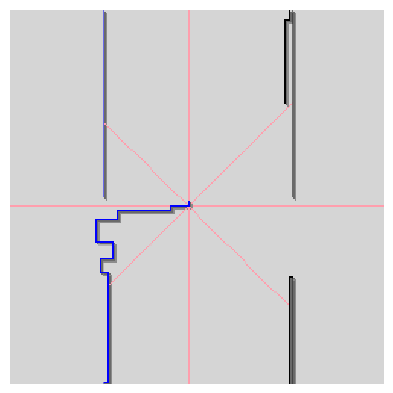
Our robots, provided with simple "sensors", perceive the world in eight directions. Each sensor evaluates the distance in pixels from the current position to the nearest obstacle in these directions: Front, Back, Left, Right, FrontLeft, FrontRight, BackLeft and BackRight (fig. 3). Every sensor returns a maximum value of 1 for an immediate obstacle (i.e. a wall in an adjacent pixel), a lower number for an obstacle further away, and 0 when there are no walls in sight.
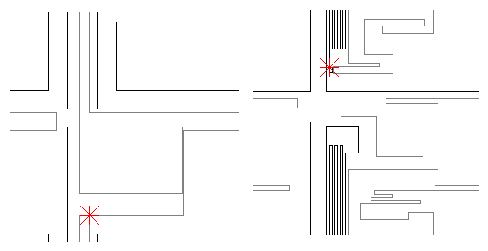
In earlier exploratory experiments (Funes, 1996), we used a Genetic Algorithm (GA) to learn the weights of a perceptron network that played Tron. It became evident that while this simple architecture is capable of coding players that could perform interestingly when facing human opponents, such "good" weights were difficult to find in evolutionary or coevolutionary scenarios. Collusion (Pollack and Blair, 1997) was likely to appear in most evolutionary runs in the form of "live and let live" strategies such as that shown in Figure 4.
2.1 System Overview
In our present work, we are using Genetic Programming (GP) (Koza, 1992) as a means for coding artificial Tron players. The set of terminals is {_A,_B,..., _H (the eight sensors) and ℜ (random constants between 0 and 1)}. The functions are {+, -, * (arithmetic operations),% (safe division), IFLTE (if a <= b then-else), RIGHT (turn right) and LEFT (turn left)}. A maximum depth of 7 and a maximum length of 512 limit the valid s-expressions. A robot reads its sensors and evaluates its s-expression every three steps during a game. If a RIGHT or LEFT function is output, the robot makes the corresponding turn; otherwise, it will keep going straight.
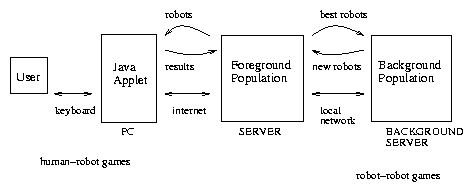
We have written a Java applet and launched our game on the Internet. The architecture of the system takes advantage of Java's ability to run a "client" on the user's local machine and a "server" on our host (Web server) machine. As shown in Figure 5, the Java Applet runs on the user's local machine; the Foreground and Background servers execute on our machine. The Tron applet receives a GP s-expression (from our server), representing a Tron-playing strategy. The applet runs, playing one game with the human user, until a crash occurs. When the game ends, the applet opens a connection to our server, reports the results of the game and receives a new s-expression for the next game. This cycle continues until the human decides to quit playing.
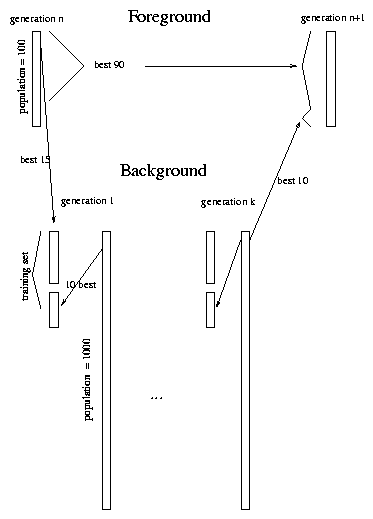
We use a two layer server architecture to maintain two separate Tron-playing artificial populations simultaneously, as illustrated in Figure 5. The Foreground Server plays games with humans, while the Background Server engages in self-play to create brand new artificial players that will be incorporated into the foreground population when the foreground process is ready for a new generation.
The interaction between robots and humans occurs at a relatively slow pace: only a few hundred games may happen every day. An evolving population idles, waiting while these games are accumulated, until there is enough information to evaluate its individuals. The role of the background process is to replace the usual reproduction stage, exploiting all this idle time to produce the best robot players that self-play can give us. Instead of raw crossover and mutations, the new individuals of the population will have been trained and filtered through self-play.
2.2 Foreground Server
The foreground portion of the Tron system controls the interplay between robots and humans. It maintains a population of 100. Every time a player requests a new game, the server supplies one of these robots at random. When a user finishes a game, the foreground process saves the outcome in its database.
A generation in the foreground process lasts until all 100 agents have played a minimum number of games. The new agents that are playing for the first time in the current generation play a minimum of 10 games, while the "veterans" that have survived from previous generations play only 5 games. When all agents have completed their minimum number of games, the generation is finished and the next generation is started.
To start a new generation, the 100 current agents are sorted by fitness. The worst 10 are eliminated and replaced by 10 fresh ones, supplied by the background process. A new generation begins.
The fitness of robots is a shared fitness measure designed to promote speciation (Beasley et al., 1993; Juillé and Pollack, 1996) by giving points for doing better than average against a human player, and negative points for doing worse than average. For each agent a, the fitness is calculated as
where l(h,a) is the number of games lost by each human opponent h against a; p(h,a) is the total number of games between the two; l(h) is the total games lost by h; and p(h) is the number of games that h has played. The measure is summed across all games played (not just those that belong to the current generation). The exponential factor on the right is a confidence measure that devalues the average scores of those humans that have played only a few games.
An inherent exploitation/exploration bias occurs when we make 10 new robots play 10 times per generation and 90 veteran agents play 5 times each. This means that 18% of the games are played by the rookie agents, who have not been evaluated yet.
2.3 Background Server
The role of the background process is to supply the foreground process with good artificial players for each new generation, the best that can be produced given the results that have been accumulated. We proceed as follows: every time the foreground population begins a new generation, the background receives the 15 fittest agents from the foreground. This group of 15 agents comprises part of a training set against which a new population of 1000 random agents is generated and evolved. When the foreground process finishes one generation, it receives the 10 best agents that emerge from this procedure, adding them to its own population, and the cycle restarts (Figure 6).
The background process plays all the individuals in its population against the training set of 25 agents. Fitness is evaluated, and the bottom half of the population is replaced by random mating with crossover of the best half. The fitness function is defined as follows:
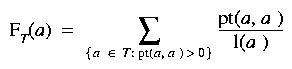 (2)
(2)
where T is the training set, pt(a, a') = {0 if a loses against a', 0.5 if they tie and 1 if a wins} and l(a') is the number of games lost by a'. Thus we give more points for defeating good players than bad players.
As indicated above, the training set consists of two parts. The first 15 members are fetched from the foreground process. The remaining 10 members of the training set are replaced each generation with a fitness sharing criteria. The new training set T' is initialized to the empty set and then new members are added one at a time, choosing the highest according to the following shared fitness function:
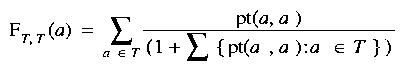 (3)
(3)
This selection function is adapted from (Rosin, 1997) and acts to decrease the relevance of a case that has already been "covered", that is, when there is already a player in the training set that beats it.
When the best players from the foreground population re-enter the background as members of the training set, their genotype is isolated: they do not reproduce explicitly. They do so only implicitly as they disfavor players they can beat, and favor players that beat them. . Scheme of foreground and background evolutionary populations.
3. Results
Our server has been operational since September 1997, and as of this writing we have collected the results of over 35,000 (animal vs. animat) games. This is a small amount compared with the number of games played by the background process, which plays 25,000 games per generation, approximately one generation per hour. We are keeping the system running, continuing to make adjustments and experiment with different ideas. The results presented here are based on the first 82 days of data, or 37,295 games.
Our basic performance measure is the win rate, that is, the fraction of games that the artificial players have won. The average win rate over the total number of games played is 0.42, meaning that 42% of all games completed have resulted in animat victories.
The graph in fig. 7 uses a sampling rate of 1000 to plot the evolution of the win rate over time. It illustrates two important factors. First, there are oscillations. This is a natural phenomenon in a coevolutionary environment, and occurs here more noticeably since one of the evolving populations consists of randomly selected human players. Each of the 416 individuals sampled here has a different level of expertise(1), has played a different number of games, and so on(2).
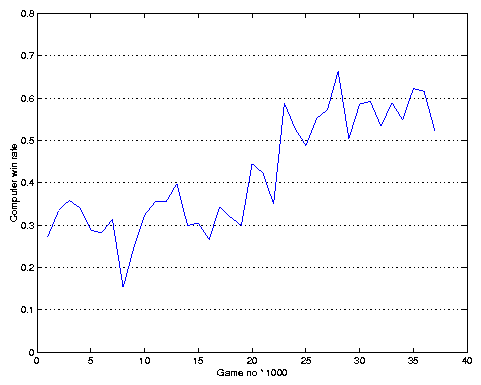
The second important feature is that there is a visible trend toward improvement. The winning rate has gone up roughly from 28% to 55% over the time that the system has been operational.
3.1 Adaptation in humans
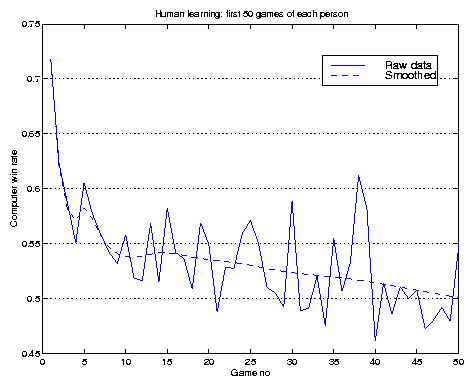
Humans learn very fast, so the Tron animats are chasing a moving target. The graph in Figure 8 illustrates the average human learning rate. A human playing his first game against our robots will have a 73% chance of losing; but by the time he has played 10 games, this expectation will be reduced to 53%. The animats win 67% of the first games, but then only 52% of the second games, etc. By the 10th game, the rate descends to 44%. (We smoothed with a moving average to show the trend over the right side of the graph.)
3.2 Adaptation in animats
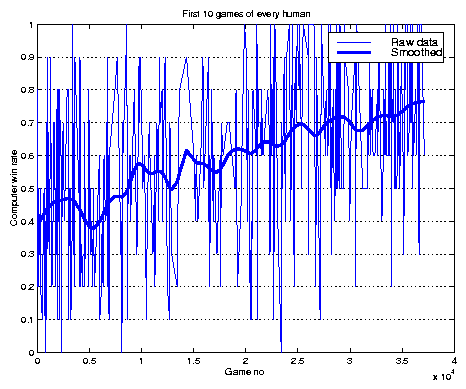
It would be desirable to factor out the influence of human learning from the data in fig. 7 in order to visualize the raw improvement of the animats. The technique of sampling suggested by (Cliff and Miller, 1995) cannot be used in this case; it is not possible to play for example `player H0001 from December 10th against robot R230001' because the human of that day is not available. Instead, we apply an averaging technique. We consider that a `virgin' user --- a human that plays for the first time --- is at the same average level of expertise no matter when he plays his first game. Examining only the first 10 games of every person who has played 10 or more games, we obtain the graph shown in Figure 9.
The raw data is very noisy since each point is the score of a single human: some players log into the Tron system for the first time and win their first 10 consecutive games, showing a computer winning ratio of 0. Others lose their first 10 games and end up with a computer winning ratio of 1. Most players perform somewhere in between. But smoothing with a moving average shows a steady trend towards robot improvement. Starting at around 40%, the computer winning ratio has increased to nearly 74%.
--------------------------------
Ranking Robot Wins/ Games
ID No. Games Played
--------------------------------
1 510006 0.87 63
2 460003 0.82 94
3 460008 0.80 94
4 400010 0.78 132
5 480001 0.78 85
6 540004 0.77 52
7 460002 0.71 94
8 330003 0.74 167
9 540006 0.74 54
10 460007 0.73 91
...
40 100009 0.60 288
...
100 150001 0.45 269
--------------------------------
Table 1: Best robots
Using our raw approximate measure (the win ratio), we obtain a score for each robot. But since luck determines the opponents of each artificial player, this ratio will only be an estimation that approaches a true value as the number of games played increases. In Table 1, we have listed the best artificial players, out of those who have played at least 50 games.
The two first digits in an robot's ID number represent the generation where it first appeared in the foreground population. The current 10 best robots belong to generations 51, 46, 40, 48, 54 and 33. Among the most veteran agents there are a few strategies born in generation 10, each with around 300 games played. The worst robot presently alive has a win rate of 0.45. Strategy 100009 is noteworthy as it maintains a steady win rate of 60% after nearly 300 games. The longest-lived agent from the original population (generation 1) lasted 334 games before being retired, with a final win rate of 39.5%.
3.3 Analysis of sample robots
Following is the GP s-expression for the current champion, R.510006:
(* _H (IFLTE _A 0.92063 _H (- (% _D (- (+ 0.92063 (IFLTE 0.92063 _F 0.92063 (LEFT_TURN))) (IFLTE (- (IFLTE _C _G (RIGHT_TURN) (LEFT_TURN)) (IFLTE (+(LEFT_TURN) (LEFT_TURN)) _G _F _G)) _H (RIGHT_TURN) _G))) (RIGHT_TURN))))
This can be roughly reduced to pseudocode as:
if FRONT < 0.92063 go straight
else if 0.92063 >= REAR_RIGHT turn left
else if LEFT < RIGHT turn right
else turn left
This robot will always go straight, unless there is an obstacle in front of him closer than 8% of the size of the arena. At this point, he will turn right or left. The use of the rear_right sensor is confusing, and its is difficult to infer from the code the actual behavior of this expression, as complex variations arise from its interactions with the Tron environment.
When inserted in a Tron arena, this code shows an interesting behavior. It will avoid obstacles, get out of dead ends and do tight turns to maximize space when in a confined space.
3.4 Analysis of Humans
We are also studying the characteristics of the human population that is playing our Tron. At present, we want to know if our Tron Web site has created an "egosystem", attracting Tron fans to our site (as opposed to other Tron sites) and enticing them to keep coming back in order to improve their ranking in our "Hall of Fame".
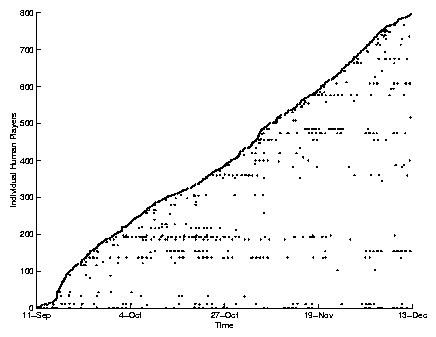
Figure 11 shows the longevity of human players, highlighting "return" players. Time is plotted along the horizontal axis, for the duration of the data analysis period. The vertical axis represents each individual human player that played any games during the time period shown. Each dot on the graph stands for one or a few consecutive games played (13 games on average).
This graph shows that players who came to the site at the beginning of the experiment are still coming back, since some horizontal lines start in the left edge of the graph and continue (though sporadically) to the right edge. The sporadicism is a positive feature because it means that players go away for a while and periodically come back to check the artificial players that have evolved since the last time and to monitor their ranking in the table of scores.
The continual rise of the left edge of the data points indicates that new players keep coming to the site at a steady pace. The implication here is that there is enough new interest in the site so that our coevolutionary space will continue to thrive.
4. Conclusions
Our experiment has succeeded in establishing an interactive space where animal and animat adaptation happen simultaneously.
Once an ecological niche is created, and by this we mean that a piece of adaptive software like our Tron game succeeds in attracting a collectivity of users, a coevolutionary arms race will occur where human and artificial learning chase each other. We can observe human learning rates by averaging all performances of players at the same levels of experience, and we can observe agent learning rates by looking at their performance over time against new incoming opponents.
The exploration vs. exploitation trade-off is linked to the problem of creating a niche. On one hand we want to offer users our best level of performance, but on the other we need to take risks with untested versions. We address this problem in two ways. First, we set our parameters so that only 18% of the games are played by rookies. Second, we exploit the slow pace of human interactions, evolving new robots in the background, so that our novice robots will be as good as possible.
Regarding the algorithmic setup, several details were chosen arbitrarily. The way the background population is reset every time the front end completes a generation is questionable, and other approaches may be better, such as not resetting it at all, or doing so when the dynamics of its own evolutionary process indicate. Genetic isolation between front and back end populations is an arguable factor, since it prevents new players from capitalizing on older genotypes.
The issue of diversity is a central point throughout our coevolutionary setup that needs to be emphasized. Shared fitness functions stimulate diversity by promoting original candidates in every new generation. Resetting the background population and genetic isolation are also promoting diversity, creating new solutions from scratch in each cycle.
Diversity and speciation are key in addressing the problem of transfer, or lack of generalization, by widening the spectrum of solutions produced by an introspective learner that needs strategies to cope with a wider environment than the one defined by a limited fitness function that describes only a few points of a larger problem.
The shared fitness function of robots vs. humans (eq. 1) addresses the problem of diversity of levels of expertise among the user population, but also attempts to prevent cooperative phenomena at this level, as robots are given points not for winning or losing, only for doing better or worse than the average of the other robots. The factor of human adaptation has not been accounted for in this function, and future versions should try to adjust accordingly, perhaps using an exponential decay factor.
As perceived by each individual user, our virtual Tron is playing differently every time, since we randomly switch Tron programs for each individual game. Simultaneously, the overall level of play is going up over time. This heterogenous behavior is part of the success; when we say that a certain robot is winning 87% of its games, this is a valid indicator of its level of play given the collective behavior of all other robots. If we were to send the same identical robot over and over, humans would quickly learn strategies against it, and the system as a whole would be boring.
There are severe representational limitations to our Tron agents due to their limited sensory perception. Whereas humans observe the entire state of the game in every screenshot, robots only "see" the nearest object in eight fixed directions. They have no perception of the position and heading of their opponents, and are incapable of analyzing the game board as a whole in order to make their decisions. Future research should contemplate a more powerful version of their sensors.
We have shown that evolutionary techniques can be successfully applied in the context of an environment of connected human users. The variable input of random players with diverse expertise and interests exhibits exploitable average trends. The trend toward collusion through cooperation in coevolutionary agents can be broken in adaptive software environments by incorporating the raw fitness evaluation emerging from its end-users.
References
Axelrod, R. M. (1984). The Evolution of Cooperation. New York, Basic Books.
Gilbert, L. E. and Raven, P. H. (eds.) (1975) Coevolution of animals and Plants. University of Texas Press.
Cliff, D. and Miller, G. F. (1995). Tracking the Red Queen: Measurements of adaptive progress in co-evolutionary simulations. In F. Moran, A. Moreno, J. J. Merelo and P. Cachon (eds.) Advances in Artificial Life: Proceedings of the Third European Conference on Artificial Life (ECAL95). Lecture Notes in Artificial Intelligence 929, Springer-Verlag, pp.200-218.
Hillis, W. D. (1992). Co-evolving parasites improve simulated evolution as an optimization procedure. In Langton, C. et al. (Eds.) Artificial Life II, Addison-Wesley. pp. 313-324.
Lieberman, H. (1997). Autonomous Interface Agents, ACM Conference on Human-Computer Interface [CHI-97], Atlanta.
Miller, G. F. and Cliff, D. (1996). Co-evolution of Pursuit and Evasion II: Simulation Methods and Results. In Proceedings of the Fourth International Conference on Simulation of Adaptive Behavior. MIT Press. pp 506-515.
Tesauro, G. (1989). Neurogammon Wins Computer Olympiad. Neural Computation I, 321-323.
Tesauro, G. (1992). Practical issues in temporal difference learning. In Machine Learning. 8:257-277.
Wolpert, D. H. (1990). A Mathematical Theory of Generalization. Complex Systems 4: 151-249.
Footnotes
- (1)
- Another variable factor is the speed of the game in the client machine, which goes down due to the low speed of Java interpreters inside Internet browsers.
- (2)
- We have called the low peak at 8000 games the "khith anomaly" because it consists mostly of games by the same one person, with login name "khith".
- (3)
- Smoothing obtained by convolution with , normalized. α = 0.25.
- (4)
- Smoothing obtained by convolution with , normalized. α = 1024.
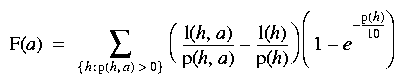 (1)
(1)