 |
DEMO Lab
|
Sevan G. Ficici |
Ofer Melnik |
Jordan B. Pollack |
| sevan@cs.brandeis.edu | melnik@cs.brandeis.edu | pollack@cs.brandeis.edu |
 |
DEMO Lab
|
We use evolutionary game theory (EGT) to investigate the dynamics and equilibria of selection methods in coevolutionary algorithms. The canonical selection method used in EGT is equivalent to the standard "fitness-proportional" selection method used in evolutionary algorithms. All attractors of the EGT dynamic are Nash equilibria; we focus on simple symmetric variable-sum games that havepolymorphic Nash-equilibrium attractors. Against the dynamics of proportional selection, we contrast the behaviors of truncation selection, (mu, lambda)-ES, linear ranking, and Boltzmann selection. Except for Boltzmann selection, all of the alternative methods we test unconditionally fail to converge onto polymorphic Nash equilibrium. Instead, we find point attractors that lack game-theoretic justification, cyclic dynamics, or chaos. Boltzmann selection converges onto polymorphic Nash only when selective pressure is sufficiently low; otherwise, we obtain attracting limit-cycles or chaos. If our intent is to solve variable-sum games with coevolution, then our results show that many selection methods are inappropriate. If our intent is to use coevolution to model another dynamical system, then our results emphasize the degree to which the model's behavior is sensitive to implementation details regarding selection -- details that we might not otherwise believe to be critical.
Selection Method |
Pressure Range |
Notes | |
| Fitness Proportional | Not Applicable | Standard in evolutionary game theory. Nash attractor, as expected. | |
| Truncation | 0 < k < 0.5 | Higher values of 'k' give higher selection pressures. | |
| 0.42 <= k <= 0.5 | converges to all Hawks, or cycles. | ||
| 0.31 <= k <= 0.41 | chaos or cyclic behavior. | ||
| 0 < k < 0.30 | cyclic behavior. | ||
| (Mu, Lamba)-ES | 0 < k < 1.0 | Lower values of 'k' give higher selection pressures. | |
| 0.59 <= k < 1.0 | chaos or cyclic behavior. | ||
| 0.42 <= k <= 0.58 | converges to all Hawks, or cycles. | ||
| 0 < k <= 0.41 | converges to all Hawks or all Doves, or cycles. | ||
| Linear Rank | Not Applicable | cyclic behavior. | |
| Boltzman | 0 < k | Higher values of 'k' give higher selection pressure. k = 0.05 ESS attractor; k = 0.2 limit cycle; k = 0.5 edge of chaos. | |
The map diagram indicates how the proportion of Hawks changes from Time t (x-axis) to Time t+1 (y-axis). Click inside the map diagram to watch an orbit of the dynamical system; the x-location of the mouse determines the system's initial condition. A cobweb diagram will be made for 500 iterations of the system. Click another position to see the orbit of a different initial condition. Use the 'clear' button to erase all orbits.
The text box below the graph indicates the numerical value of the last orbit's initial condition. You may also specify any desired initial condition by typing directly into this text box. Initial conditions can be specified as floating-point numbers, e.g. '0.5', or as fractions, e.g. '1/2'.
Please see paper for details:
Ficici, S.G., Melnik, O., and Pollack, J.B. (2000) "A Game-Theoretic Investigation of Selection Methods Used in Evolutionary Algorithms." In Proceedings of the 2000 Congress on Evolutionary Computation. Zalzala, A., et al (eds.). IEEE Press.
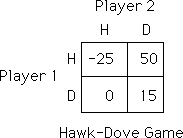
Written by Sevan G. Ficici
v0.2 (4/30/2000)
Copyright (C) 2000 by Brandeis University Board of Trustees
Software License